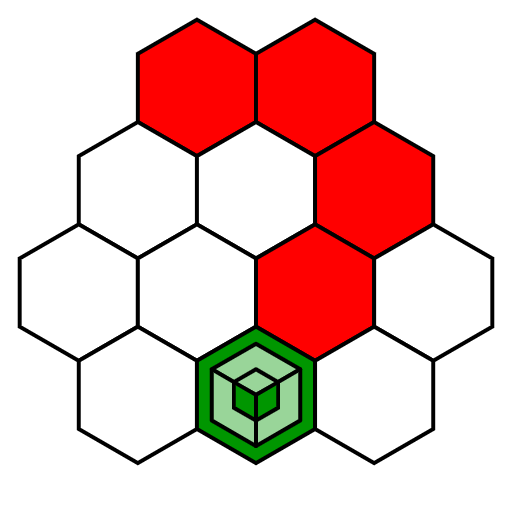
This is one of the easiest Triloop puzzles on the site. See the Triloop page for further description of the rules, or see the walkthrough below the puzzle.
Note that this sample puzzle, as well as all puzzles on this site, is live and playable. Click between a pair of dots to create a line segment that connects them (and set its color), or click an existing line segment to remove it. You can also draw a path from dot to dot across any number of dots, and then set the color for that path.
First, we’ll cover the basics, and then provide a detailed walkthrough.
The Basics
This puzzle is solved by drawing three loops on the grid, one of each color, so that they properly surround the clues. For example, the yellow clue in the top left of this puzzle must be inside the yellow loop, but must not be inside the red or blue loops. The other clues similarly describe the loops that must (and must not) surround that clue.
Note that the orange clue has the regions for red and yellow filled in, since those are the two primary colors that combine to make orange. You can simply use the presence/absence of these three regions to solve any puzzle, if the actual colors pose a challenge for any reason.
Two loops can cross each other, but cannot simply touch at a corner.
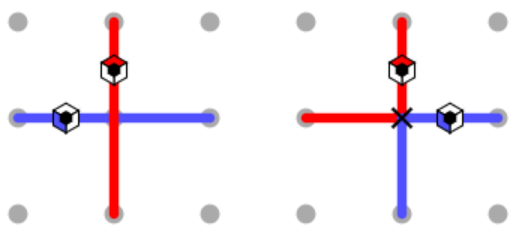
Detailed Walkthrough
Any clue on the edge of the grid must be inside a loop, so we can draw those loop segments on the outside. Also, the white clue must not be inside any loop, so we can extend the red path to avoid it. We can then extend the red path along the top, since the red loop cannot touch or cross itself.
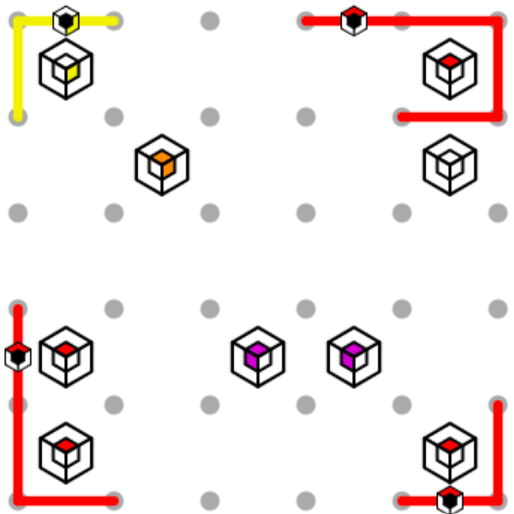
The orange clue must be inside both the red loop and the yellow loop. Since it’s inside the red loop, there must be a red edge over it somewhere. That edge cannot be at the top of the puzzle, because it would meet the yellow loop there and there would be no room for both paths to continue. Using similar logic on the left, we know that the red path makes a corner at the interior.
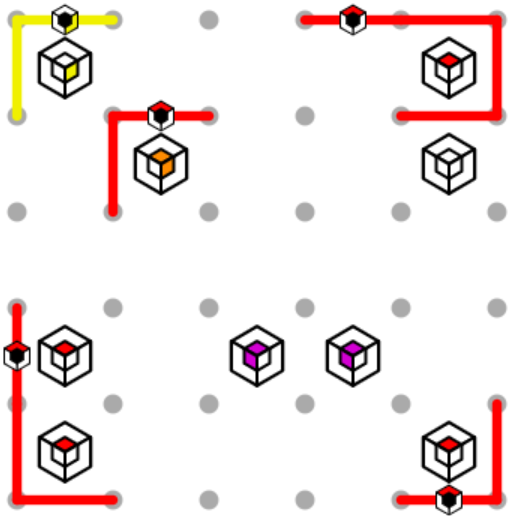
At the top of the puzzle, the yellow path is going to have to head downwards and cross the red path somewhere. It can’t head down right away, both because it would miss the orange clue and because two paths can never meet at opposite corners. It can’t extend two intersections farther, because there would be no room for both the red and yellow paths to continue. Therefore, we know it extends exactly one intersection farther, and then heads down. Then, since we know it can’t make opposite corners with the red line it is about to meet, both lines must pass through that intersection.
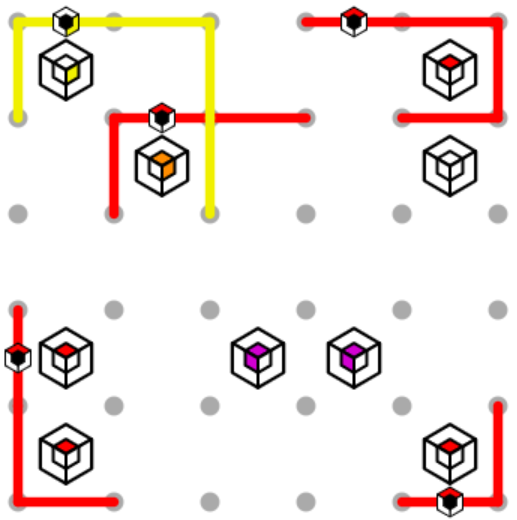
Now, we can apply the same logic for the left edge of the yellow loop. Note that the loop now fills with yellow and satisfies that yellow clue. We can also make a little extra progress on the red loop, by connecting the top and left sections in the only way possible, and can then extend the right side of the path down since no loop can touch itself.
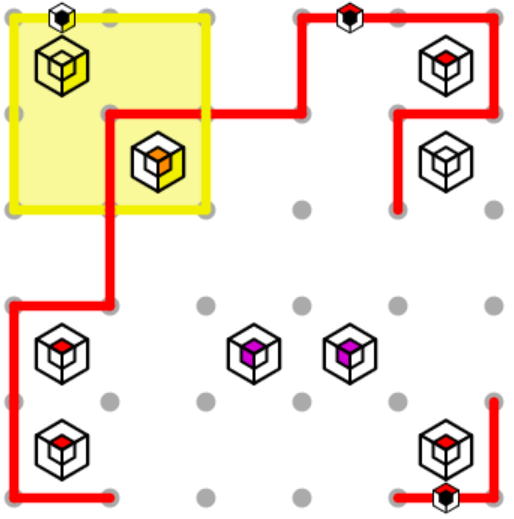
Now it’s time to tackle those two purple clues. We need to enclose them in both the red loop and the blue loop. We can start solving for the blue loop by marking with x’s where we have established corners near the loop, since the blue path cannot make corners opposite to these. We can also note that the rightmost purple clue is next to the corner, and can use the same logic we used to start the orange clue.
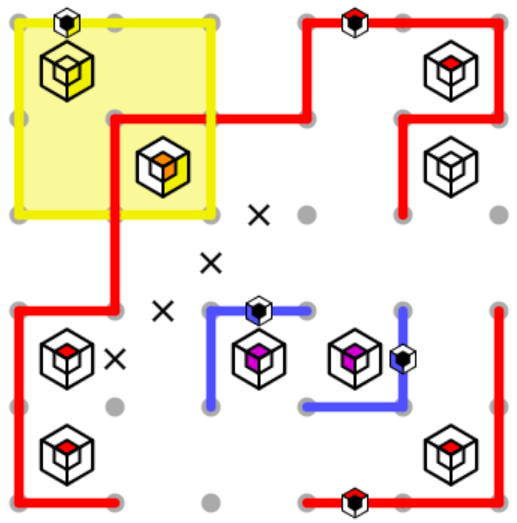
From here, we can observe that the only way for the red loop to approach the blue loop (without further violating the corner rule) would be for the red endpoint near the middle of the bottom edge to travel upwards between the purple clues, at which point they could not both be purple. So the red loop avoids the blue loop entirely, and there is therefore only one way to finish those two loops.
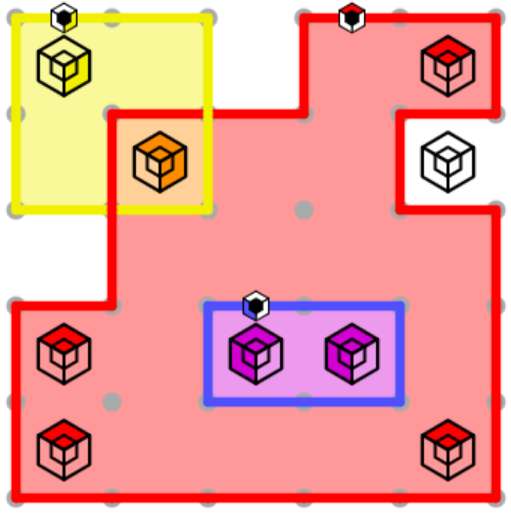
When you see the clues spinning, you’ve solved the puzzle!